平常我们所用的标准四则运算表达式,如:29+3-2(10-3)/5,叫做中缀表达式,今天介绍一种不需要括号的后缀表达法,我们也把它称为逆波兰(Reverse Polish Notation ,RPN)表示。后缀表示式为栈数据结构的一种应用。
- 中缀表达式: 2 * 9 + 3 – 2 * (10-3) / 14
- 后缀表达式: 2 9 * 3 + 2 10 3 – * 14 / –
其中上面的中缀表达式和后缀表达式等价。
后缀表达式遵循以下规则
- 从左到右遍历中缀表达式的每一个数字和符号。
- 若是数字就输出,即成为后缀表达式的一部分。
- 如果是符号,则判断其与栈顶符号的优先级,是右括号或已有栈顶符号优先级(乘除优于加减)大于等于此符号则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
现在演示 2 * 9 + 3 - 2 * (10-3) / 14 到 2 9 * 3 + 2 10 3 - * 14 / - 转换的过程
- 第1个符号为数字,所以输出 2

- 第2个符号为 * ,因为目前栈为空栈,所以直接进栈

- 第3个符号为数字 ,输出9,现在为 2 9

- 第4个符号为 + ,目前栈顶符号 * 优先级大于等于 + ,所以出栈并输出 + 符号进栈,现在的总输出为 2 9 *

- 第5个符号为 3 ,输出 3,现在为 2 9 * 3

- 第6个符号为 – ,栈顶符号 + 优先级大于等于 – ,所以 + 出栈输出 – 进栈,现在为 2 9 * 3 +

- 第7个符号为 2 ,输出 2 ,现在为 2 9 * 3 + 2

- 第8个符号为 * ,栈顶符号 – 优先级不大于等于 * ,所以 * 直接进栈,现在为 2 9 * 3 + 2

- 第9个符号为( ,直接进栈,现在为 2 9 * 3 + 2

- 第10个符号为 10 ,输出10,现在为 2 9 * 3 + 2 10

- 第11个符号为- ,栈顶元素为(,直接进栈,现在为 2 9 * 3 + 2 10

- 第12个符号为3 ,输出3,现在为 2 9 * 3 + 2 10 3

- 第13个符号为) ,此时我们需要匹配左括号(,依次出栈直到找到左括号位置,现在为 2 9 * 3 + 2 10 3 –

- 第14个符号为/ ,栈顶元素为*,优先级大于等于 / ,所以 /出栈 *进栈,现在为 2 9 * 3 + 2 10 3 – *

- 第15个符号为 14 ,此时中缀表达式已经没有需要运算数字,所以栈中的符号依次出栈,现在为 2 9 * 3 + 2 10 3 – * 14 / –

以上就是中缀表达式转化为后缀表达式的全过程,后缀表达式的计算结果遵循如下规则
- 从左到右遍历表达式的每个数字和符号,遇到数字就进栈,遇到符号就将处于栈顶两个数字出栈,进行运算,运算的结果再进栈,以此类推直到得到最终结果。
以下为演变示例图
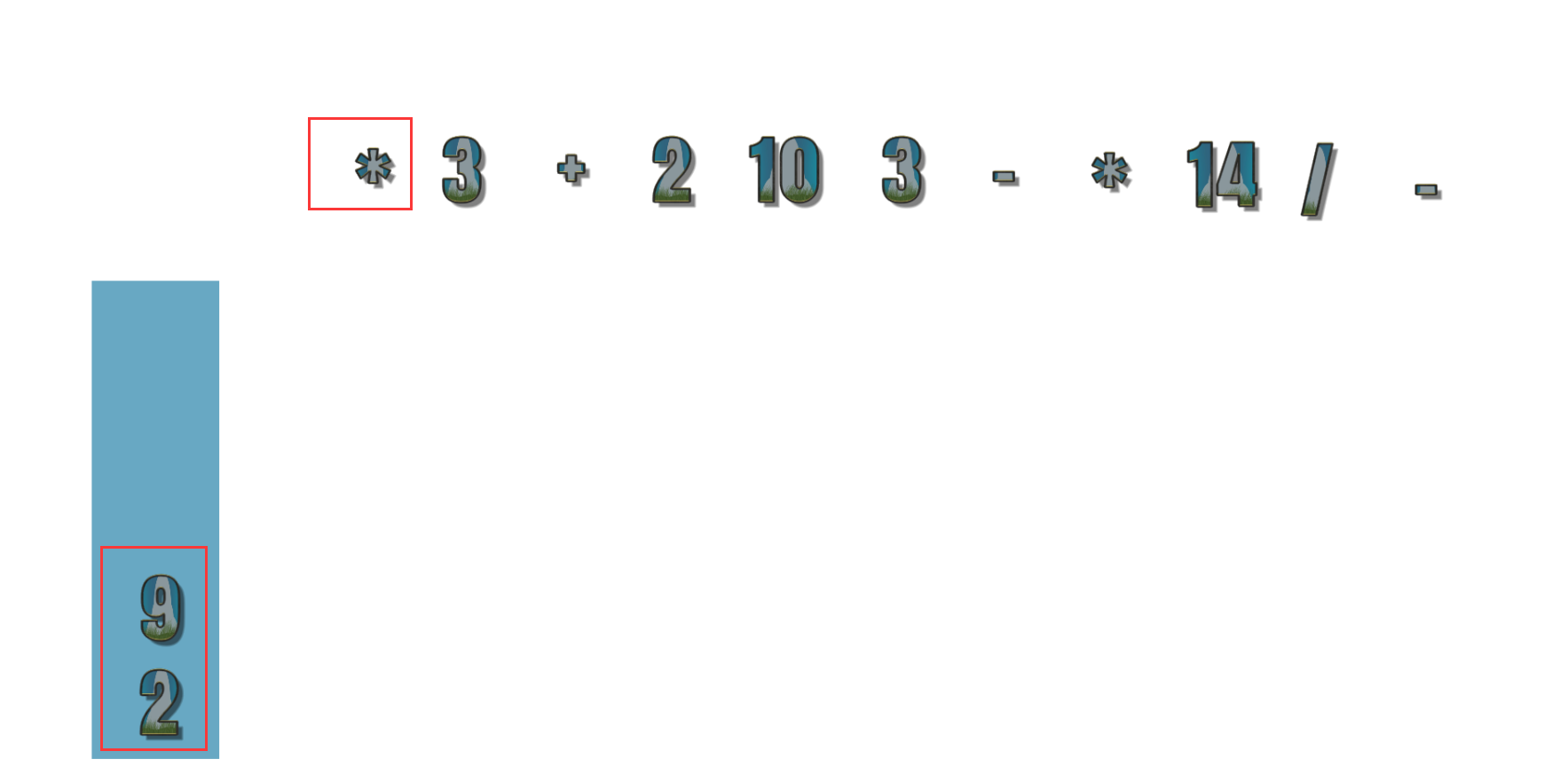
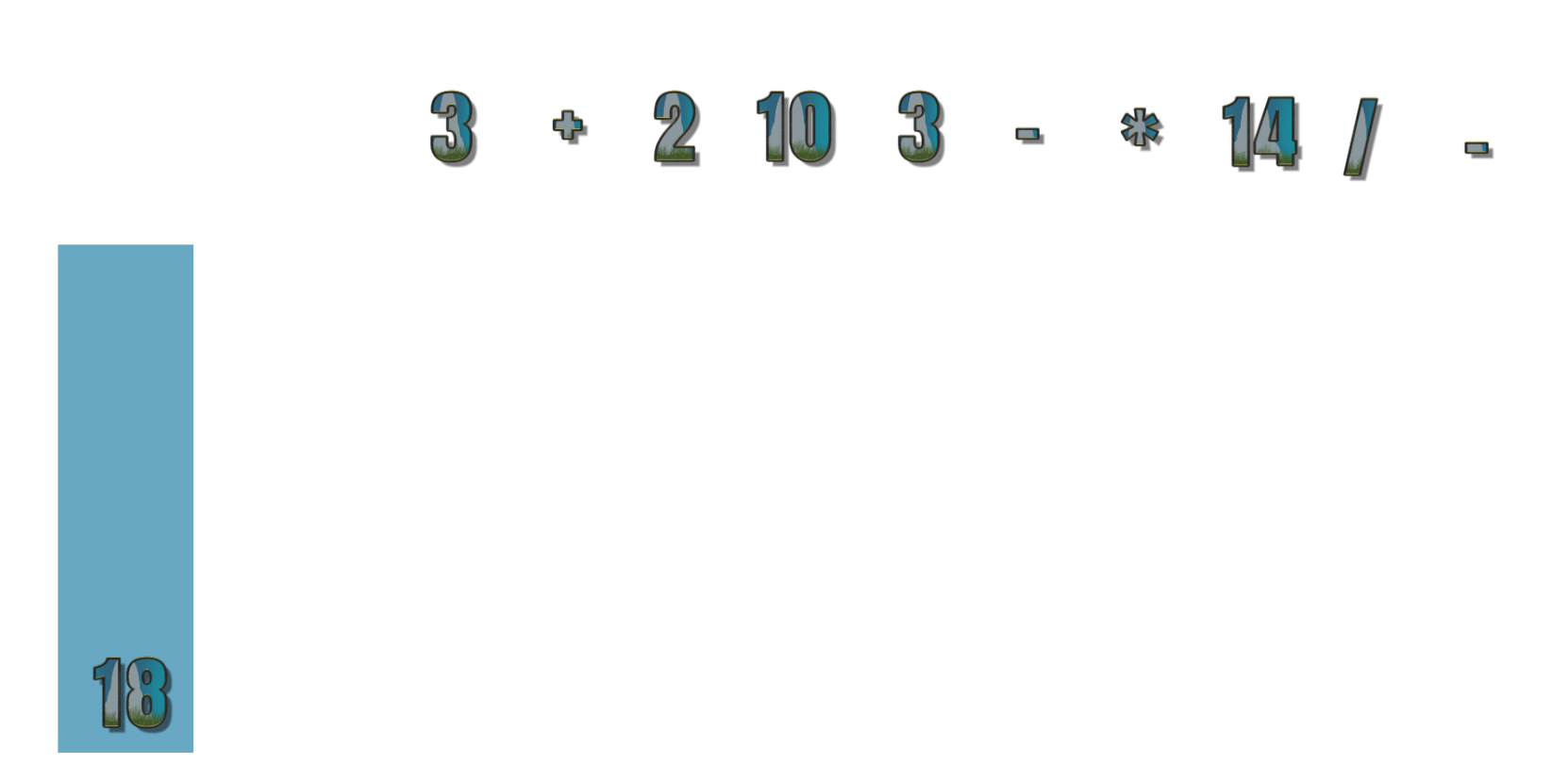

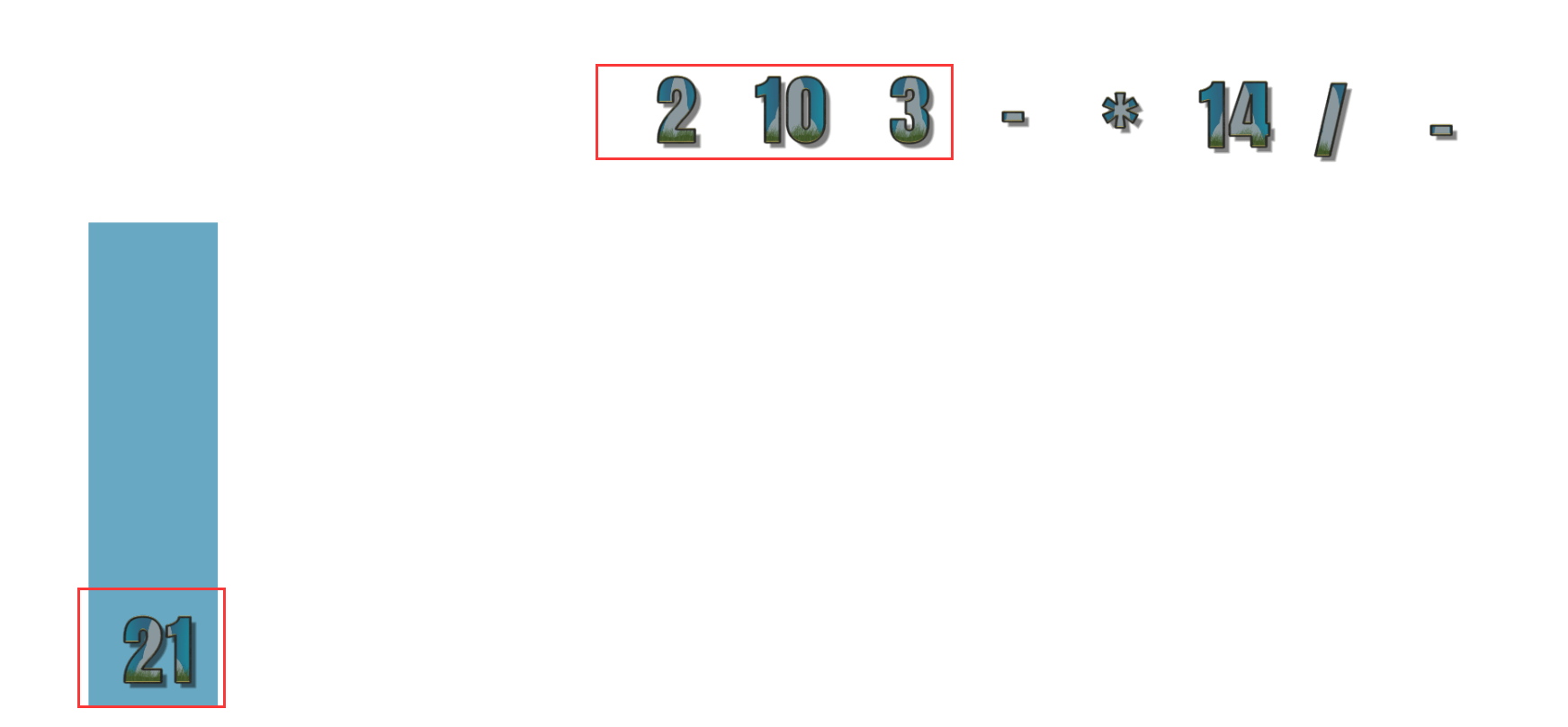





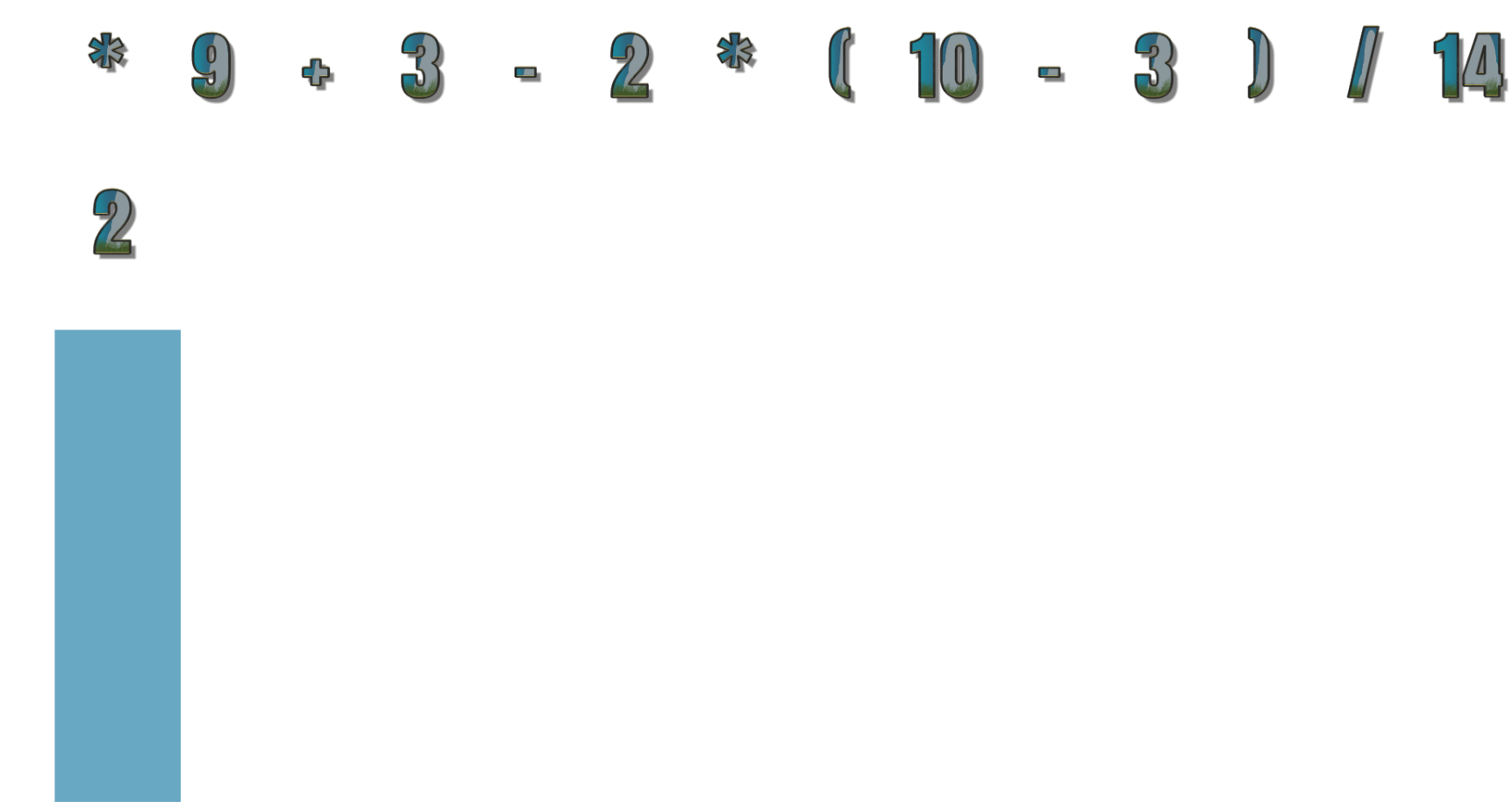
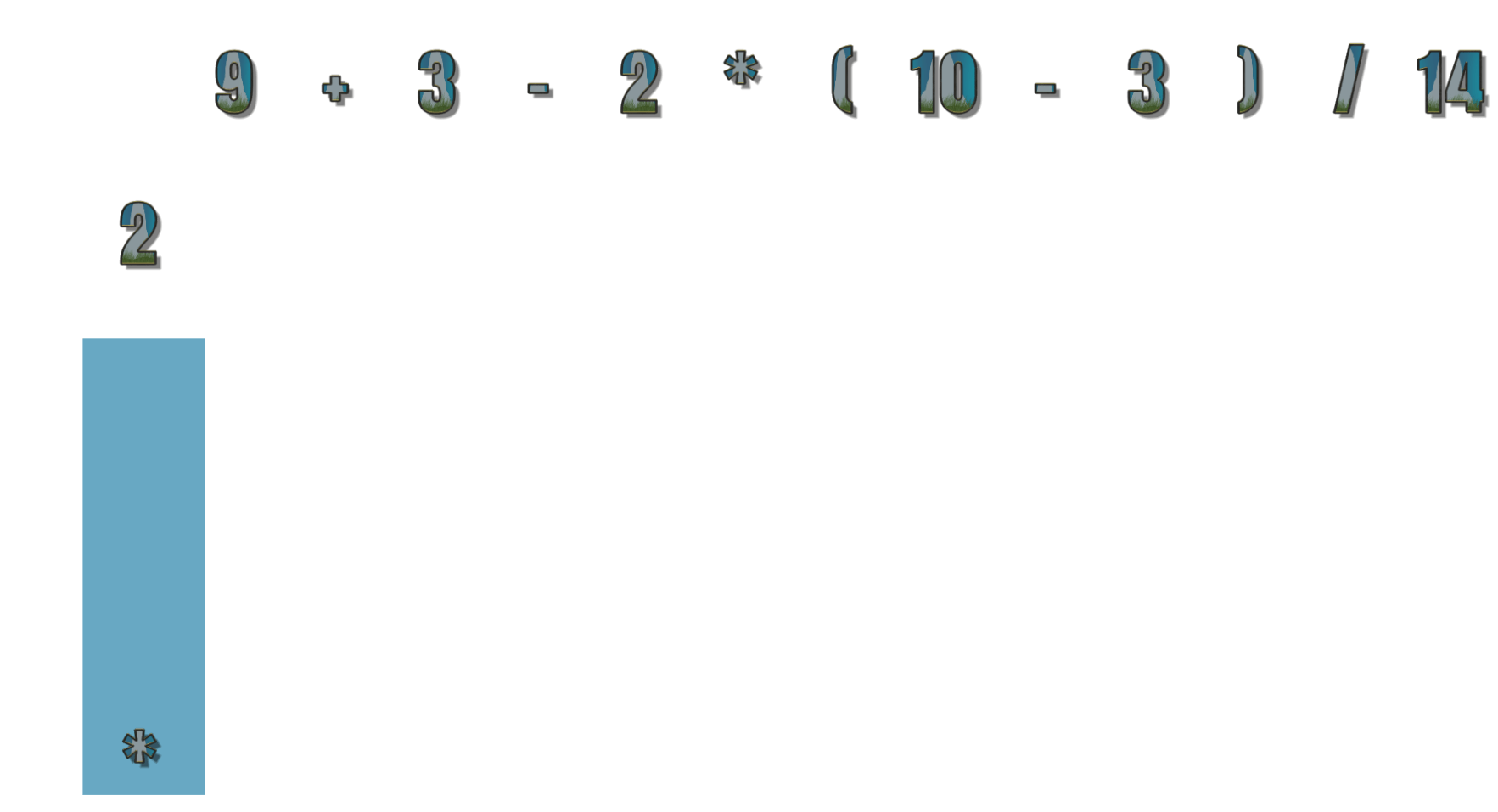
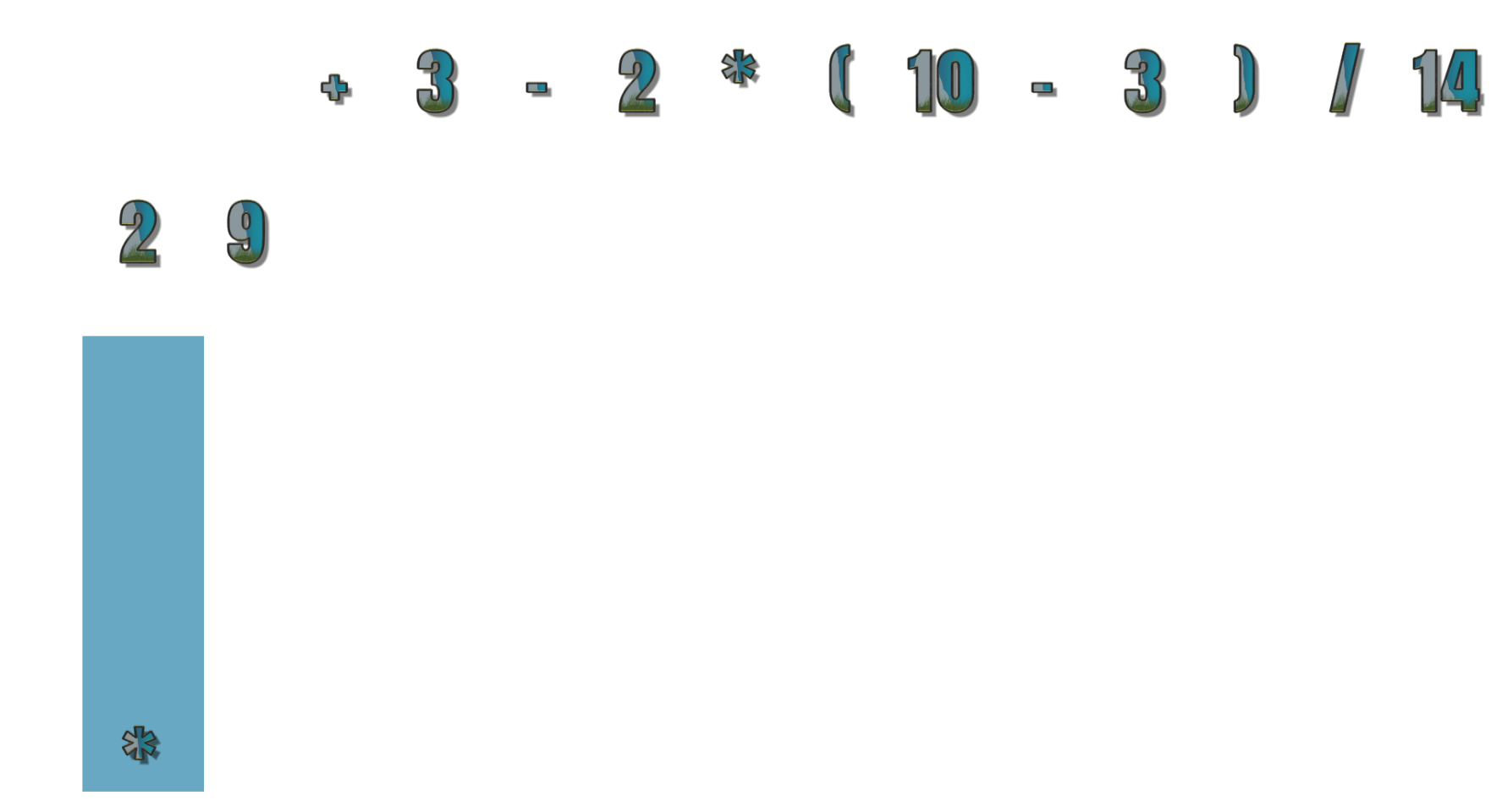
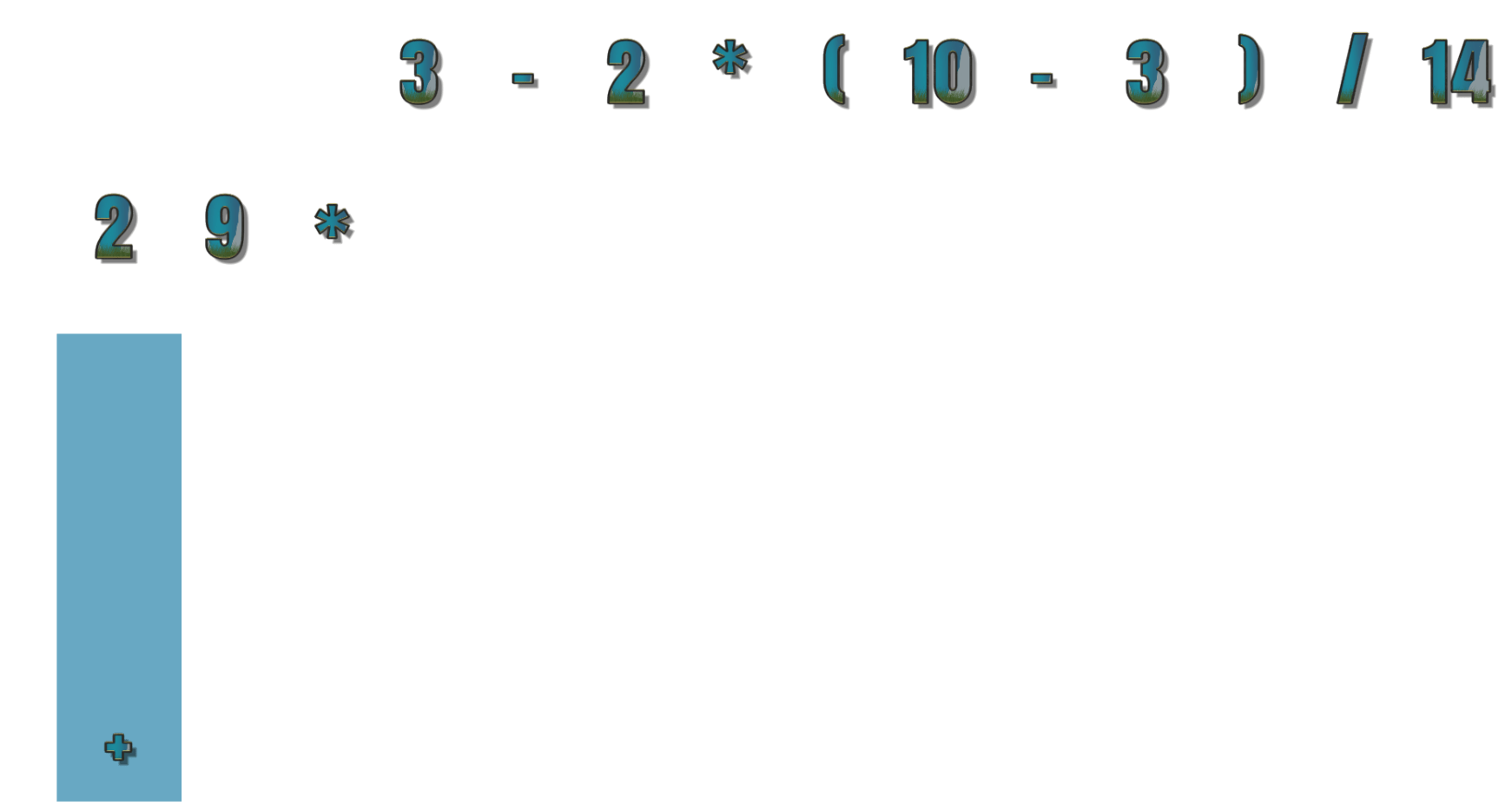
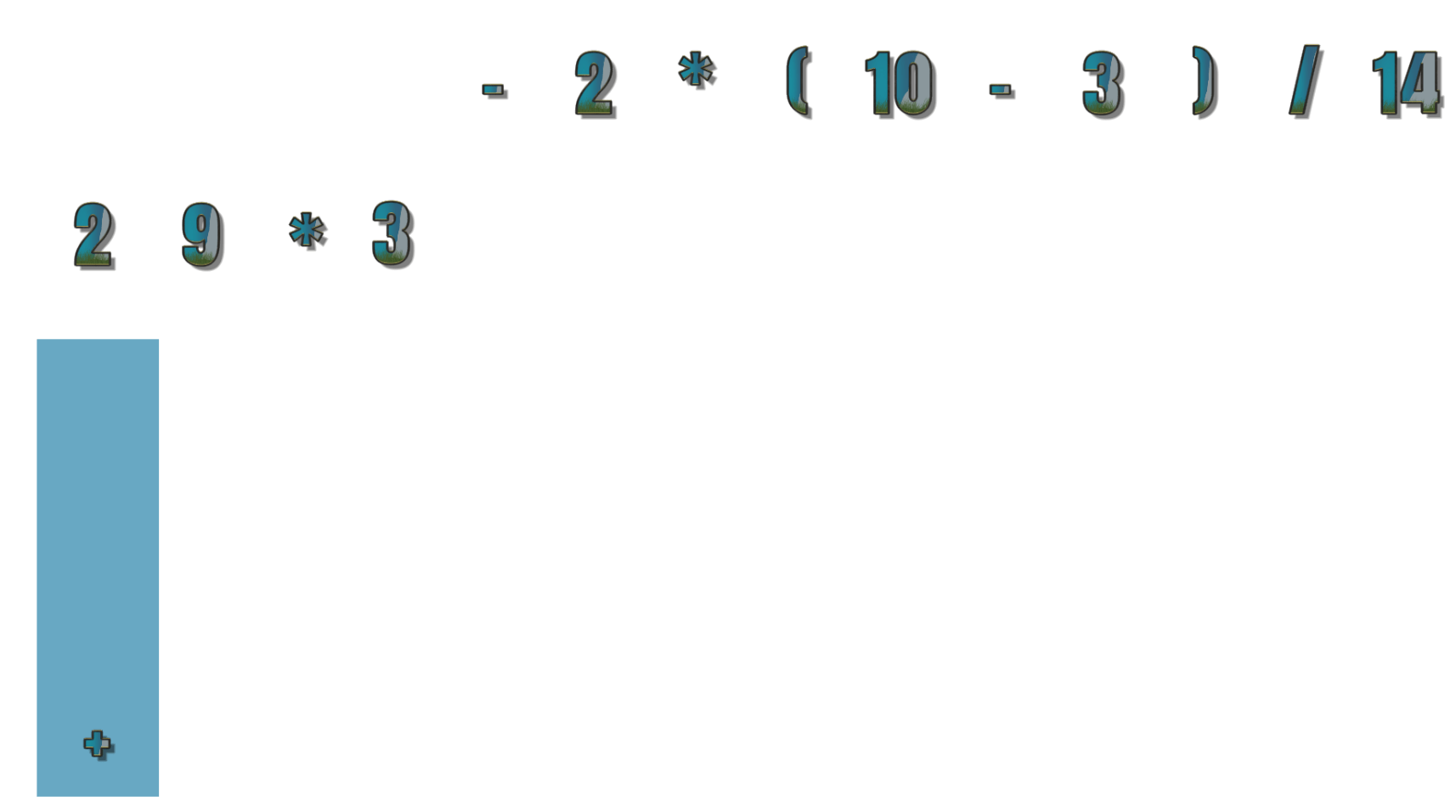
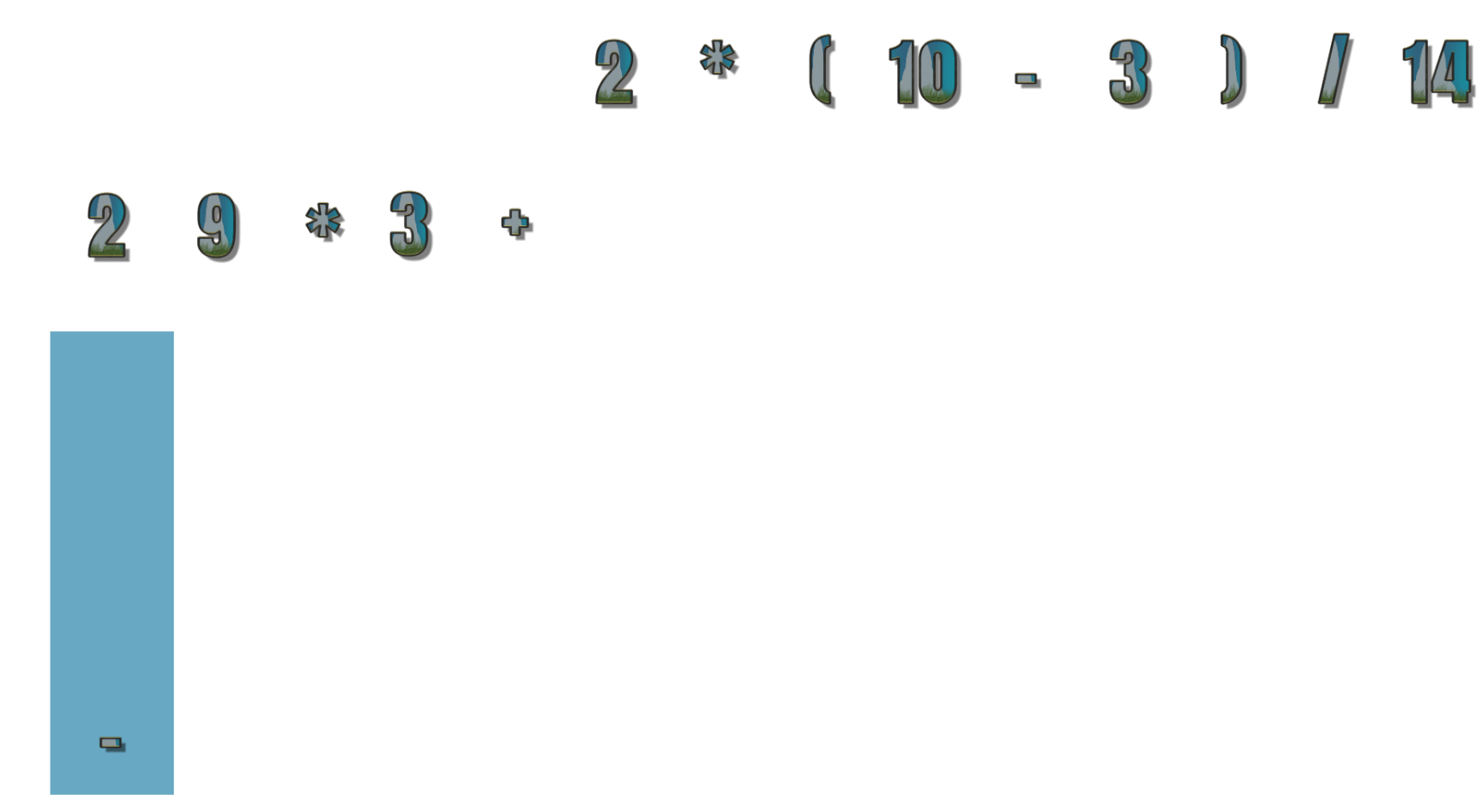
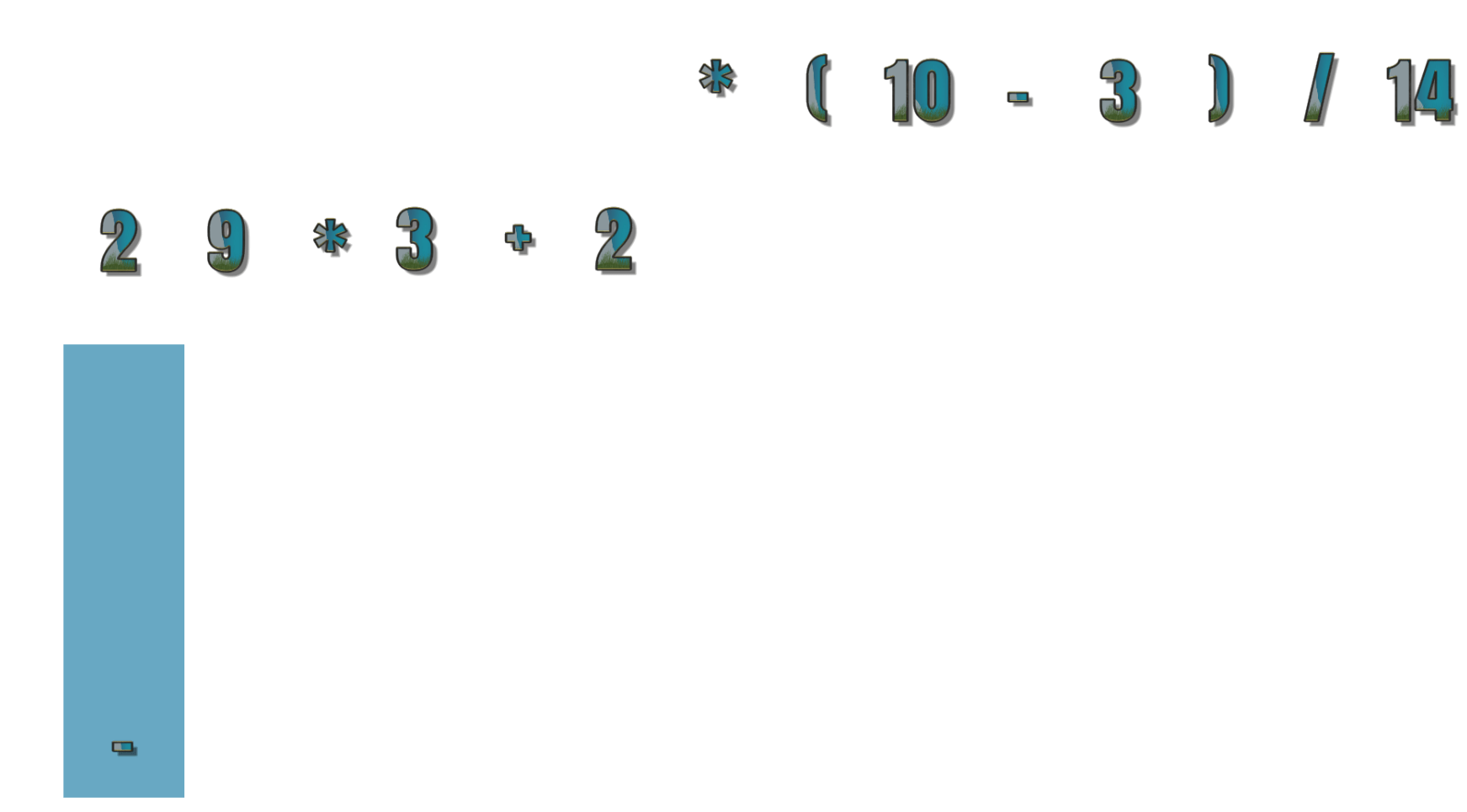
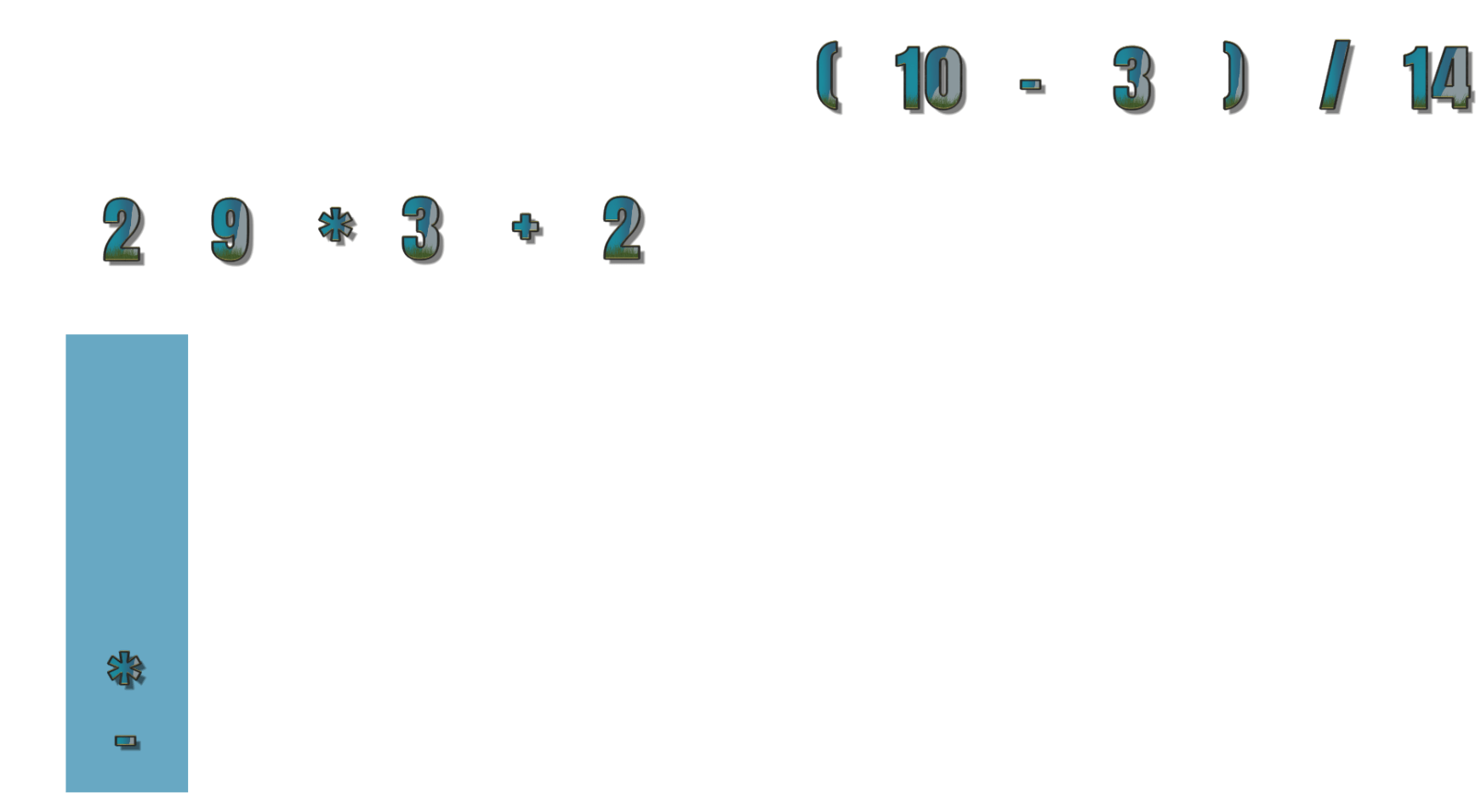
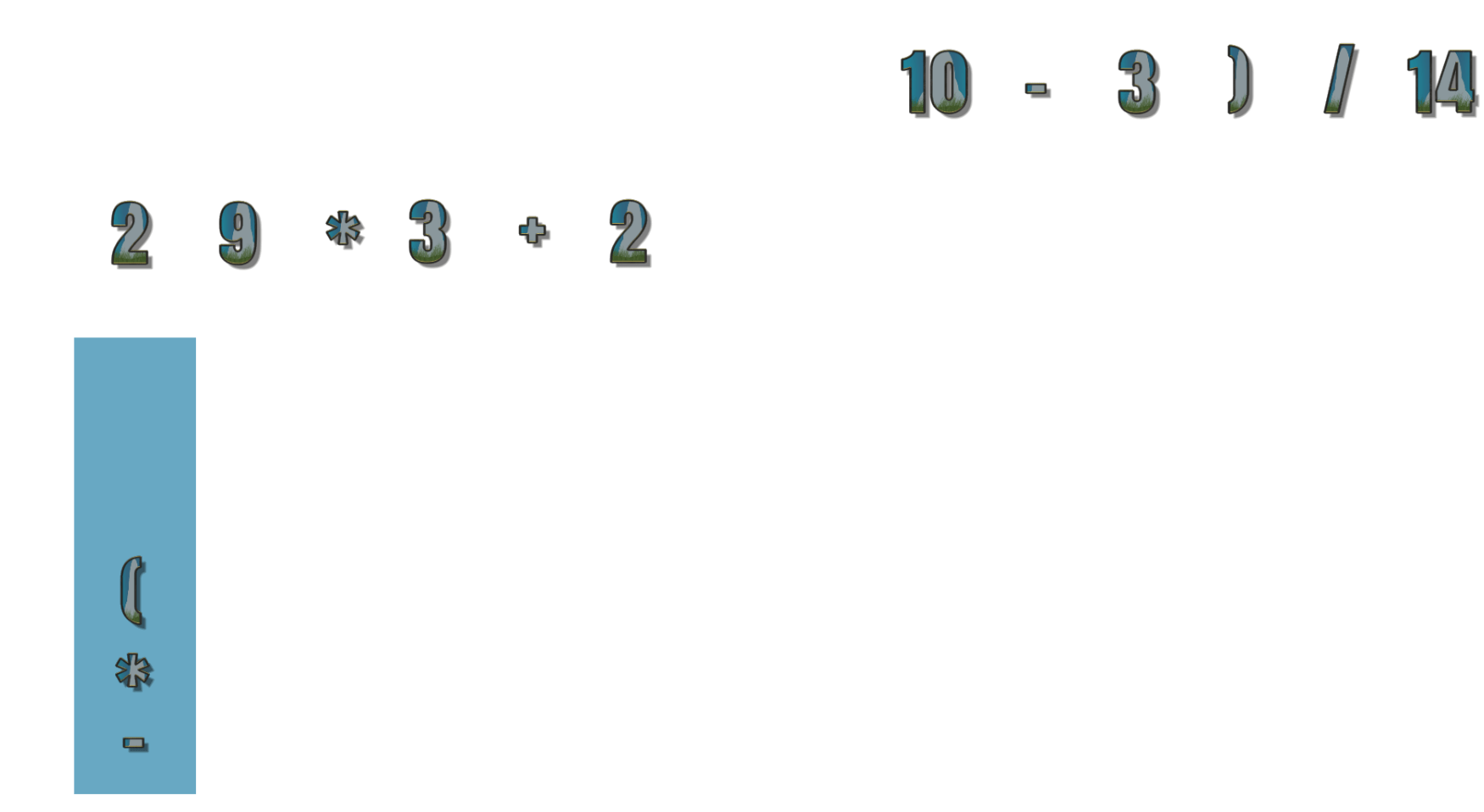
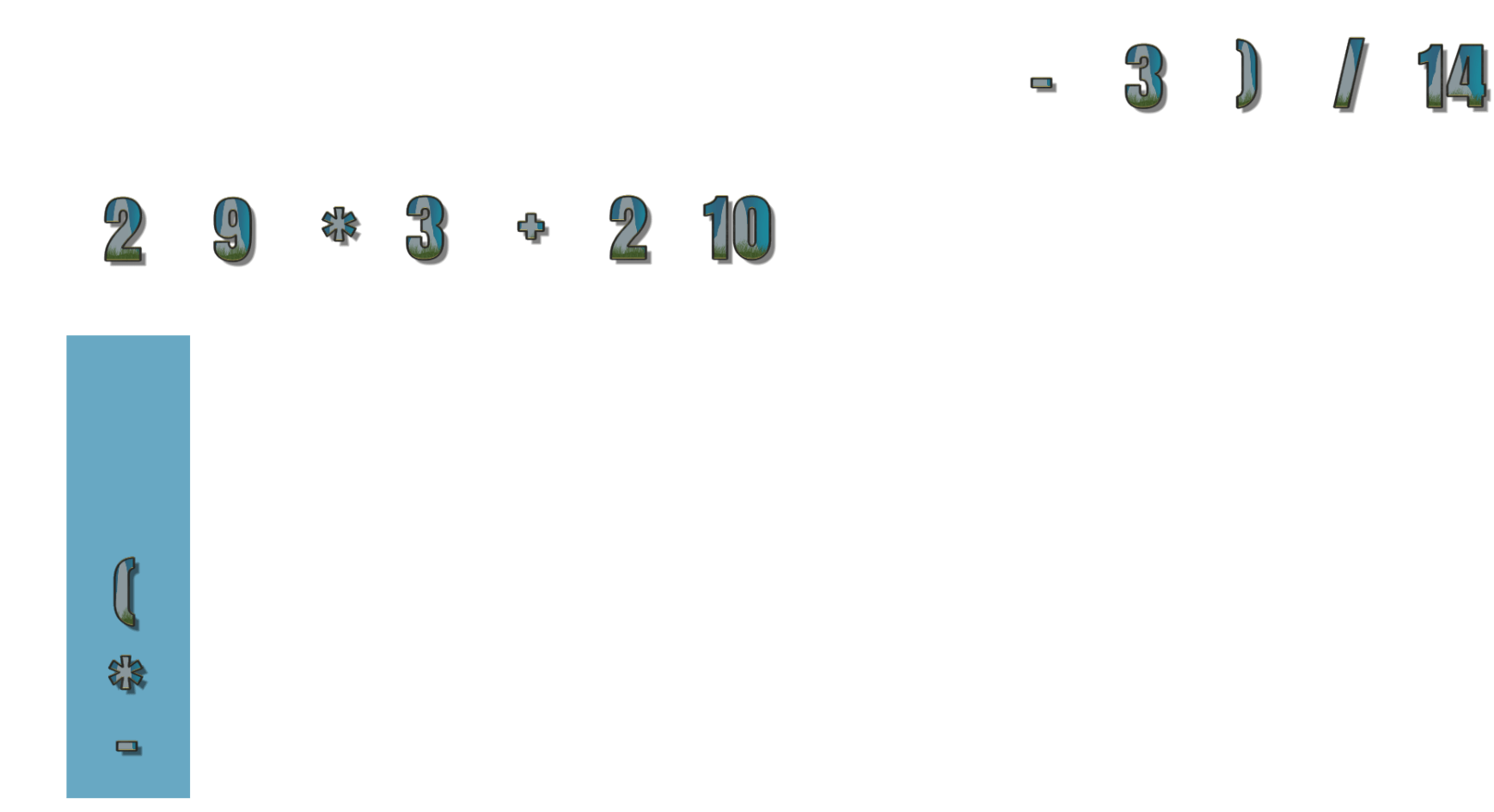
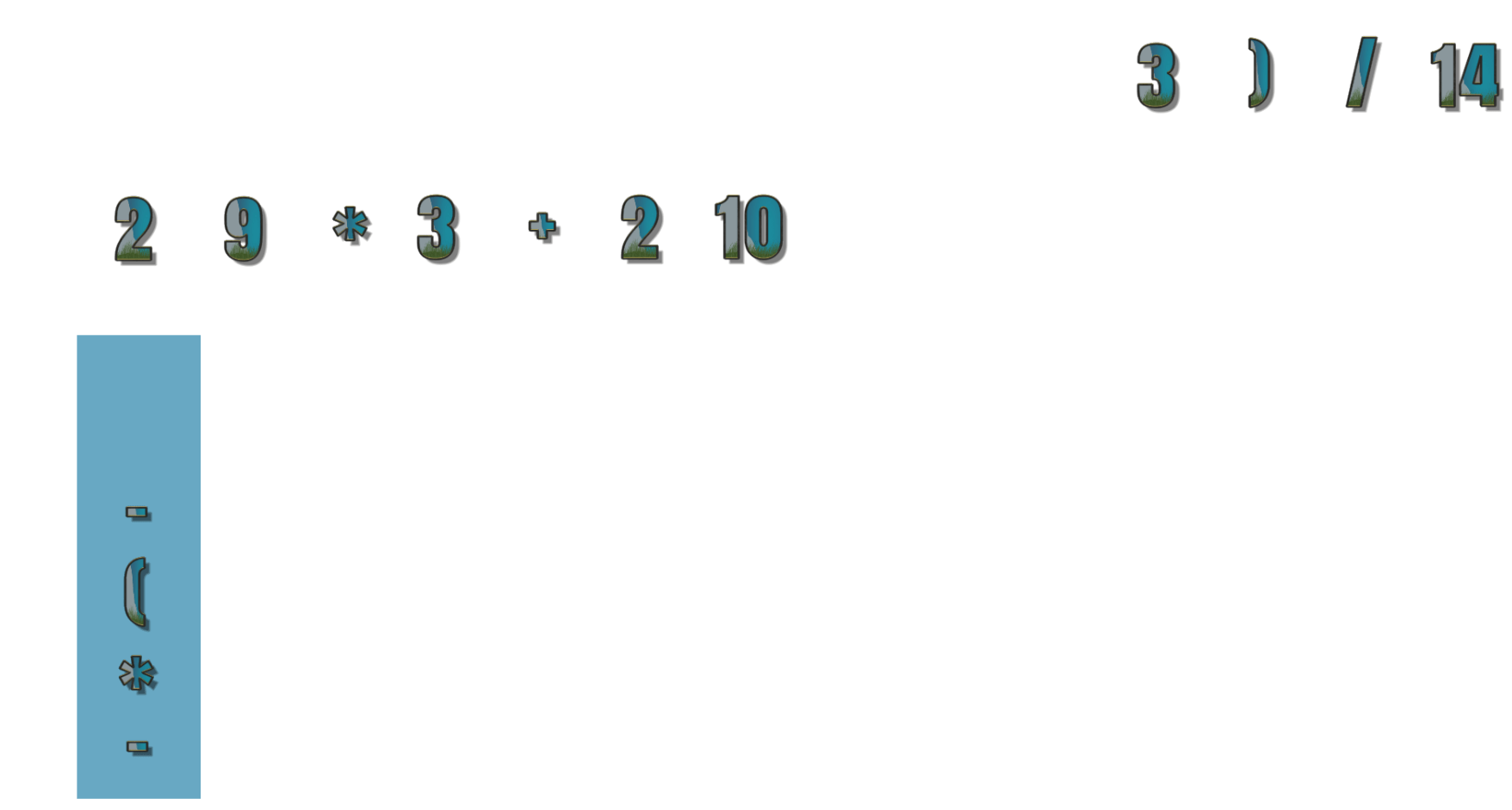
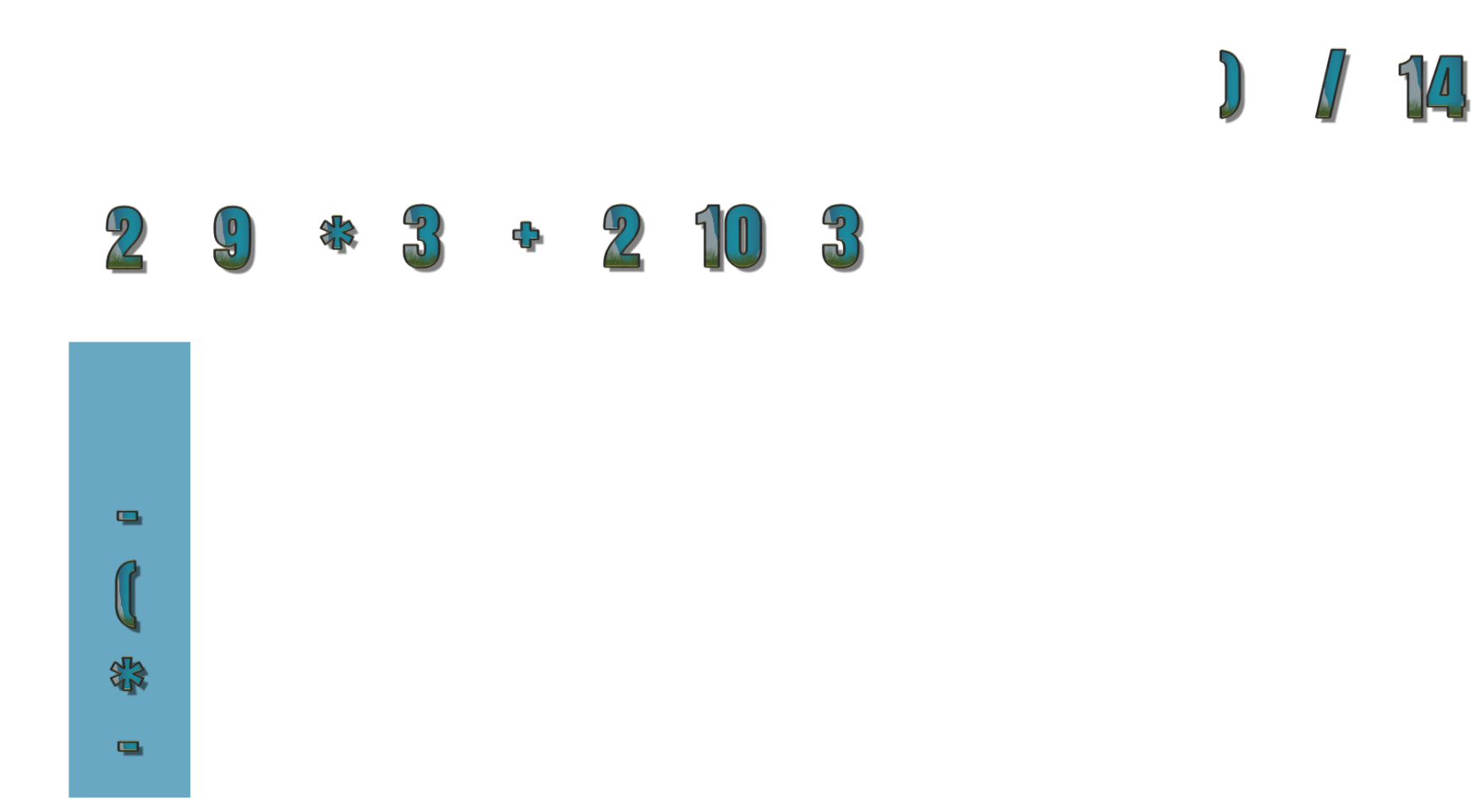
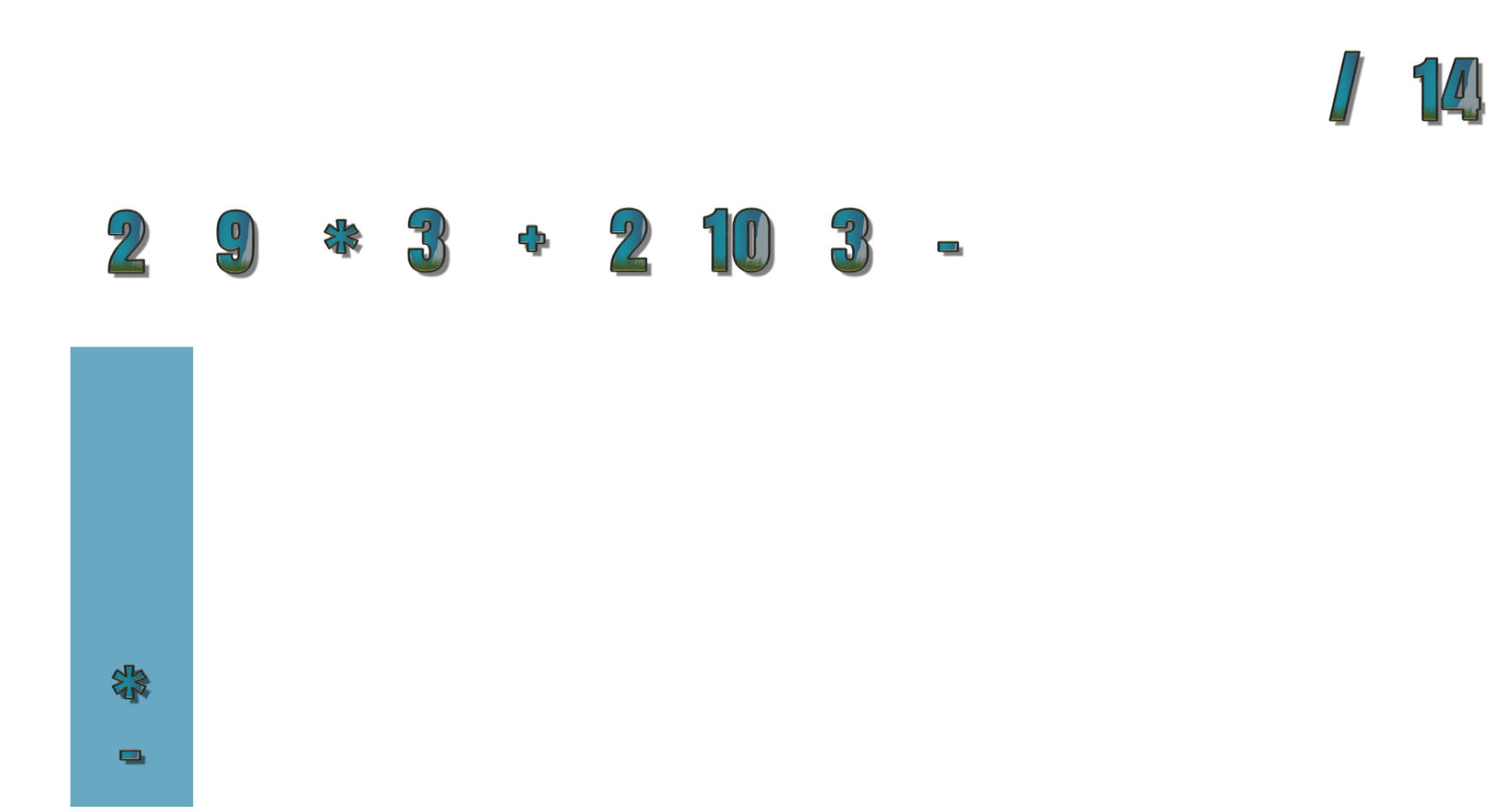
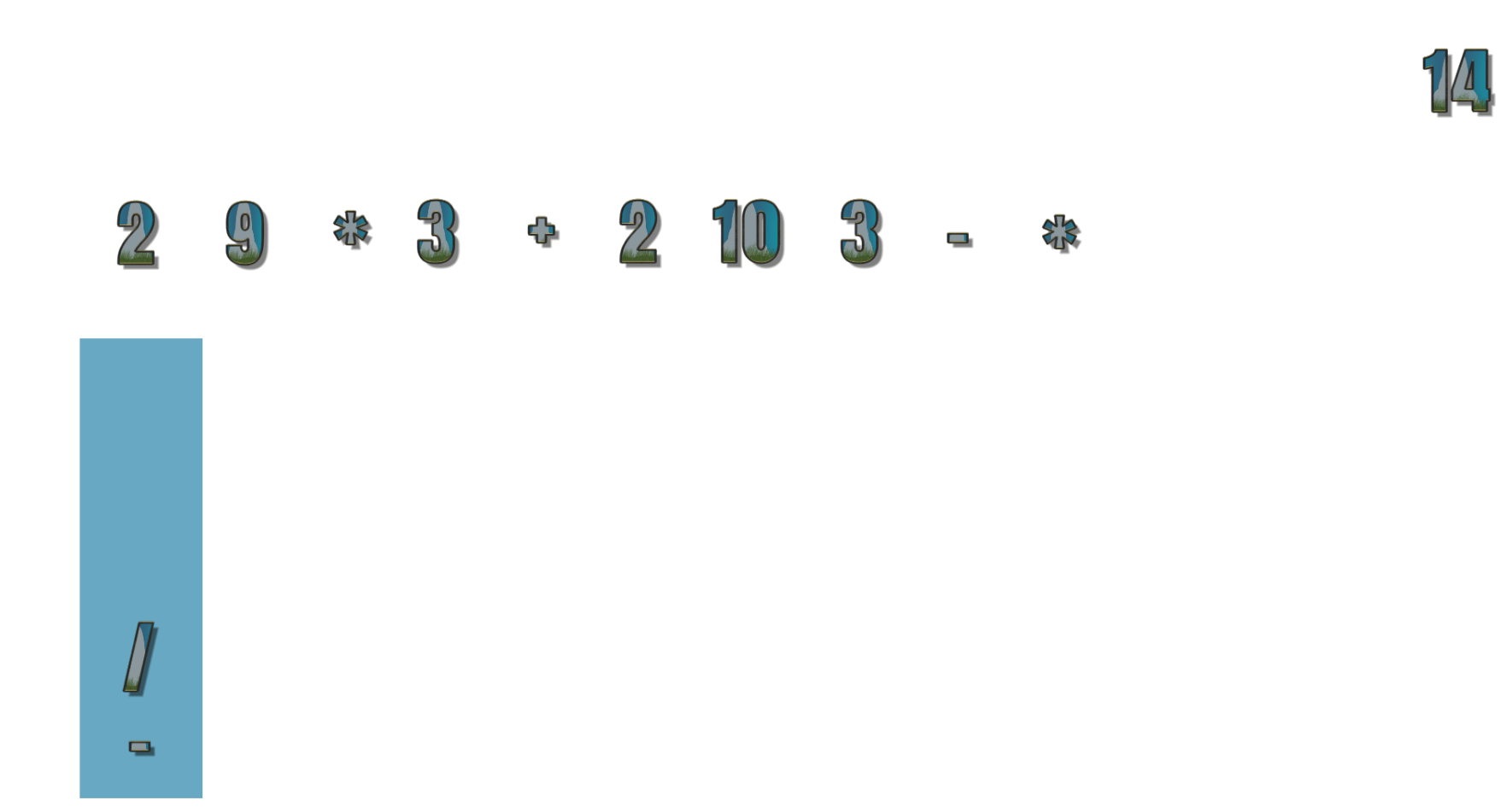
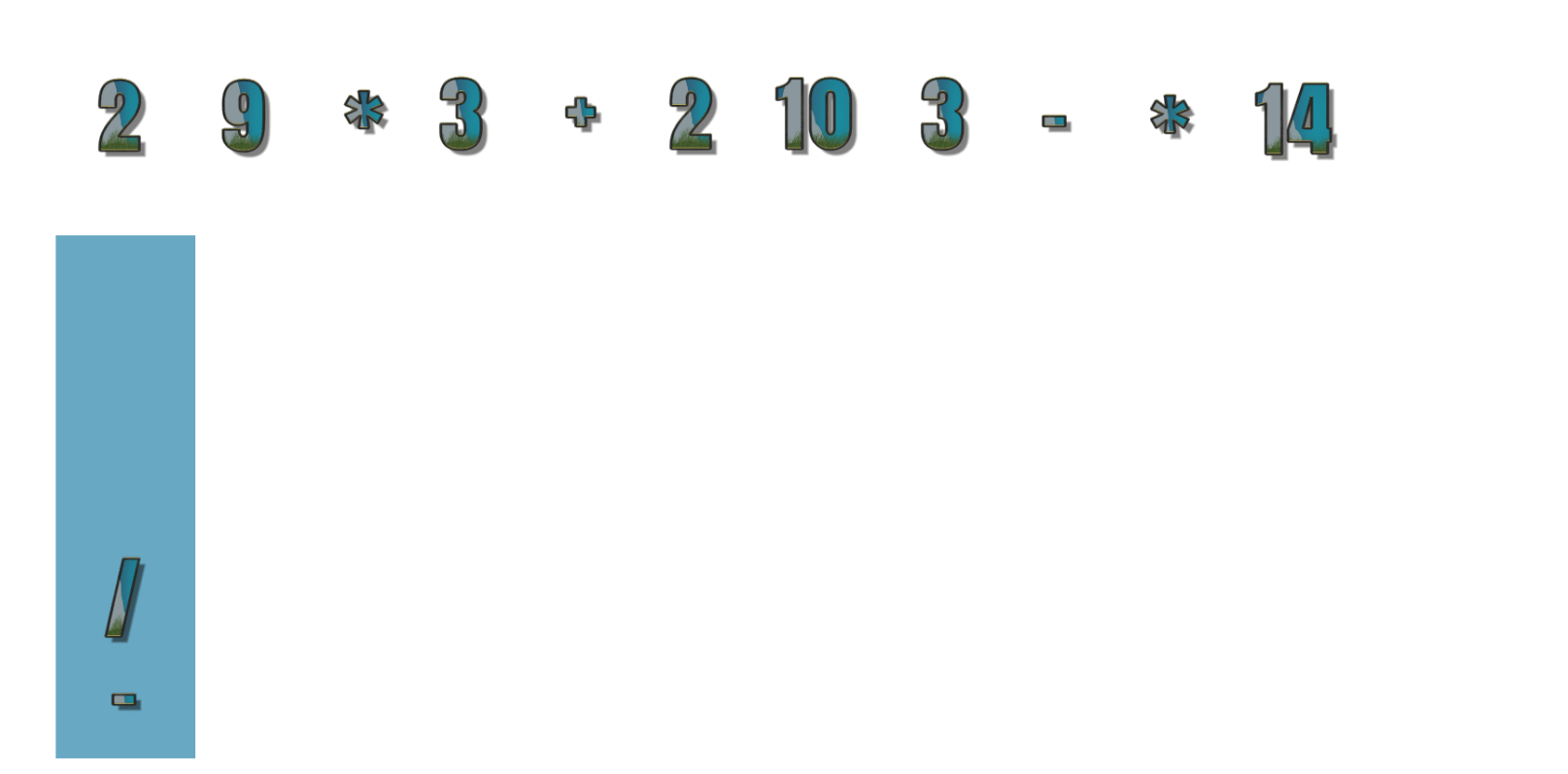
好文章,但第14步写反了,应该是“*出栈 /进栈”。